welcome_to

Construction of a triangle environment (GSP): Click here to download. Two identical shapes make up a rectangle environment (GSP): Click here to download. Hair ribbons and Wanda's cake problems (Excel).

Pet store 1 (Excel) and Pet store 2 (Excel) environments.

Mad Minute (Excel) environment for addition and subtraction. Mad Minute multiplication (Excel) environment. The Multiplication Table (Excel) environment.

Fair game (Excel) environment.

Examples of final projects for the course completed by MST students: Lesson plan 1; Lesson plan 2; Lesson plan 3, Observation & Lesson Plan 2 ; Lesson Plan 3; Classroom Observation 1; Classroom Observation 2, Classrom Observation 3, Classroom Observation 4, Classroom Observation 5

Comments to homework assignments.

Comments to homework assignments.

1) Task. Use two-color counters, and find all of the ways to make 9 in two parts. Make a chart to record the parts you found.

What are educational objectives of this task?

Use patterns to discover commutative property of addition. Use concrete objects to represent and solve problems.

Learning commutative property and multiple representation of numbers. Developing a system in intuitive strategies.

Overhead and non-overhead representations. Different concrete materials, chart representation/ recording of data

Key ideas: reasoning, multiple representations, operations, uncertainty

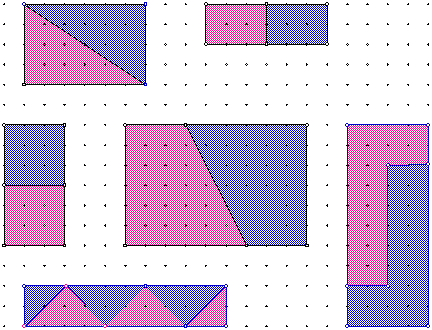
2) Task. I used two identical shapes to make a rectangle. What might they have been?

Grades 1-2:

Objectives and performance indicators: demonstrate the concept of one-half (one-half may have different meaning); mathematical reasoning; modeling/multiple representation; using concrete materials to model spatial relationships; explore symmetry.

Grades 3-4

Mathematical reasoning; modeling/multiple representation; using physical materials, pictures and diagrams to explain mathematical ideas; the use of the geoboard.

Grades 5-6

Emphasis on right angle; performance indicator - properties of polygons to classify them.

3) Task. Find ways to add consecutive counting numbers in order to reach sums between 1 and 15. For example, 3+4+5=12 and 3, 4, and 5 are consecutive counting numbers.

3=1+2; 5=2+3; 6=1+2+3; 7=3+4; 9=2+3+4; 9=4+5; 10=1+2+3+4; 11=5+6; 12=3+4+5; 13=6+7; 14=2+3+4+5.

What about 4 and 8?

Questions about the sums of consecutive counting numbers.

1. How many sums are possible for different numbers?

2. How many triangular numbers are there in the range 1 through 15?

3. What numbers in the range 1 through 15 have more than two such sums?

4. Which number in the range 1 through 15 has the largest number of different sums of consecutive counting numbers?

5. Which numbers in the range 1 through 15 can not be represented as such sums?

6. Which numbers in the range 1 through 15 have more than two addends in such sums?

7. How many square numbers are in the range 1 through 15?

8. Is it true that the larger the number, the more represetations as a sum of consecutive counting numbers it has? Why or why not?

Textbook, p. 431 (Realistic percent problems and nice numbers).

Problem 2. The baseball team won 80 percent of the 25 games it played this year. How many games were lost?

Solution. If the team won 80% of the games, it lost 20% of the games (as 80%+20%=100%). What is 20%? In fractional form it is 1/5. One has to find 1/5 of 25. The answer is 5 (games were lost).

Problem 3. In Mrs. Carter's class, 20 students, or 66 and 2/3 percent, were on the honor roll. How many students are in her class?

Solution. What is 66 and 2/3 percent as a common fraction? By shading 66 and 2/3 cells on a 100-cell grid one can see that it is 2/3.

If 20 students are 2/3, then how many are 1/3? Clearly, half of 20, that is 10. Because 2/3 and 1/3 make a whole, 20 students and 10- students make the whole class of 30 students.

Note: a formal approach to this problem would be to divide 20 by 66 and 2/3 percent? But how does one know whether to multiply or to divide? Informal approach to this problem is based on mathematical reasoning and understanding the meaning of numbers involved.

Problem 4. Zane bought his new computer at a 12 and1/2 percent discount. He paid $700. How many dollars did he save by buying it a discount?

Solution. This is an examle of a problem when no direct operation with the two numbers given enables for a correct solution of the problem. First, one has to convert 12 and 1/2 percent into a common fraction. What nice percentage numbers do we know? 25% is such an example and it is equal to 1/4. But 12 and 1/2 is just half of 25 and, therefore, is a half of 1/4. A half of 1/4 is 1/8.

Discount is 1/8 of the whole price which we do not know. Divide this imaginary whole price into 8 equal parts. Then seven-eighths is $700. What is one-eighth? We are lucky to have a nice number - the answer to the last question is $100. This is our discount. That is, George saved $100 and the whole price for his new computer was $800. No direct operation with 700 and 1/8 (12 and 1/2 %) results in $100.

Another 3 problems.

a) In the set of 60 calculators, 16 calculators are TI-81s, 29 calculators are TI-84s and the rest of calculators are TI-92s. What percent of the calculators is TI-92s? What is the ratio of TI-92s to the rest of the calculators?

Solution. 16+29=45 (both 81s and 84s); 60-45=15 (TI-92s). 15/60=1/4=25% (TI-92s); the ratio of TI-92s to the rest of the calculators is 15/45 or 1/3 (alternatively, 1:3).

b) Kelly's class of 30 students has 18 boys. What is the boys to girls ratio in the class? After spring recess three girls were transferred to another school. What is the girls to boys ratio in Kelly's class now?

Solution. Clearly, there are 12 girls in the class. So the boys to girls ratio is 18/12=3/2 (or 3:2). After spring recess there were 9 girls and still 18 boys . Now, the girls to boys ratio is 9/18=1/2 (or 1:2).

c) Ron was given 1/3 of the collection of 15 counters. 3/5 of what he got turned out to be the only red counters in this collection. How many counters were red? What is the ratio of red counters to non red counters in what Ron has gotten?

Solution. 1/3 of 15 is 5. 3/5 of 5 is 3 - the number of red counters. The ratio is 3 to 2.